By Marshall Chasin, AuD

Introduction

Frequency transposition, frequency shifting, and frequency compression are all terms that refer to algorithms that lower the frequency above a certain start point using either linear or non-linear processing.  Many manufacturers have their own terminology for their algorithm and, in some cases, manufacturer’s software will include it as a default setting for their first-fit algorithms.  In this article I will be using the phrase “frequency transposition” generically, to refer to shifting a range of frequencies to a lower frequency range. 1-3 A short-cut to quickly assessing cochlear dead regions can be found in Chasin (2019). 4

Music Is Not Speech

For speech, frequency transposition works very well, but music is not speech. Music is made up exclusively of notes and their harmonics. Harmonics need to occur at exact frequencies, not sharp and not flat. Using frequency transposition will alter the frequency of a range of harmonics and this altered harmonic structure would be, at best flat, and at worst highly dissonant. In contrast for speech, those sounds that are frequency compressed are the higher frequency ‘s’ and ‘sh’ sounds; sounds that are broadband noise or sibilant in nature, and not at “exact” frequencies. It doesn’t matter whether a sibilant sound may have a broad band of frication centered at 4500 Hz or 4200 Hz.

The following three examples can illustrate this potential difficulty: A flute and an oboe, or for that matter, a flute and a violin, or a flute and a tuba, have identical harmonics at exactly the same set of frequencies; and in the case of the tuba, the harmonics are exactly several octaves lower. For those of you who like science, each of these musical instruments are called “half wavelength resonators,” and, unfortunately, they are still called “half wavelength resonators” even if you don’t like science. This means that when a flute (or a violin, or a tuba, or a wide range of other musical instruments) plays A (440 Hz), the second space on the treble clef, there are a range of harmonics at multiples of 440 Hz; namely 880 Hz, 1320 Hz, 1760 Hz, and so on.  In order to be on key (and not sharp or flat), the harmonics need to be exactly at 880 Hz, 1320 Hz, and 1760 Hz and not flat at 850 Hz, 1300 Hz, and 1700 Hz, for example.

Even reducing a higher frequency harmonic by ½ one semi-tone, frequency transposition can completely destroy the music and only the word “dissonance” would describe it. Clinically, it is better to just reduce the amount of hearing aid amplification in this frequency region (ie, the third audio file), rather than try to change its harmonic relationships.

The first audio file is an “A-B-A” comparison.  This means that the first part of the audio file (A) is a violin playing A (440 Hz), the second part (B) is the same violin sound but with a slight application of frequency transposition where the higher frequency harmonics (above 1500 Hz) are only decreased by ½ of one semi-tone, and the third part (A) is the original unaltered violin again, for comparison.  Clinically, frequency transposition is commonly used to create changes far in excess of only ½ of one semi-tone.

The second audio file is again an “A-B-A” comparison but this time actual full orchestral music is used and not just an individual note.  Again, the same frequency transposition is applied only above 1500 Hz and only ½ of one semi-tone. Note the dissonance in the early part of the B section as the music goes up a scale.  And the final “A” part is the same as the original unaltered music.

The following spectrum shows the subtle difference that was created by just lowering the harmonics above 1500 Hz by one half of one semi-tone. The blue colored lines are for the unaltered original sound, and the white colored lines are for the slightly frequency compressed altered sound. (This can be thought of as a piano keyboard with the left hand side being the bass notes and the right hand side being the treble notes/harmonics.)

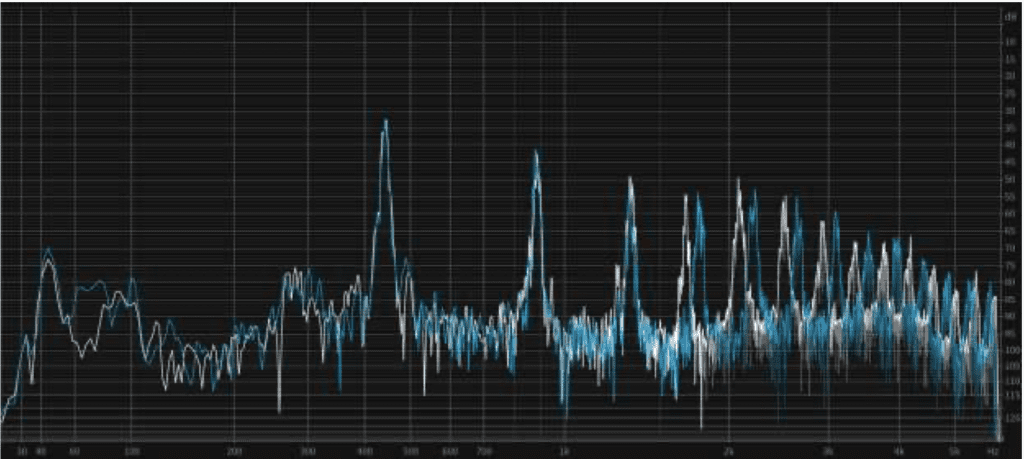
Figure 1: The blue colored lines are for the unaltered original sound and the white colored lines are for the slightly frequency compressed altered sound.

The third audio file is again an “A-B-A” comparison like the first audio file except that the harmonic energy above 1500 Hz has been gradually reduced in amplitude by rolling off everything by 6 dB/octave, instead of applying frequency transposition. This is not perfect but this gain reduction is a better clinical approach whenever one wants to avoid dissonance associated with a cochlear dead region for music.

In part two of this series, “An Island of Refuge”, the possible exception of a one octave linear transposition may be an interesting exception despite the creation of a perfect fifth and a minor third in the transposed music.

References

  1. Baer T, Moore BCJ, Kluk K. Effects of low pass filtering on the intelligibility of speech in noise for people with and without dead regions at high frequencies. J Acoust Soc Am. 2002;112(3):1133.
  2. Moore BCJ. Dead regions in the cochlea: Conceptual foundations, diagnosis, and clinical applications. Ear Hear. 2004;25(2):98-116.
  3. Moore BCJ. Testing for cochlear dead regions: Audiometer implementation of the TEN(HL) test. Hearing Review.2010;17(1):10-48.
  4.  Chasin M. Testing for cochlear dead regions using a piano. Hearing Review. 2019;26(9):12.