Acoustic feedback occurs in all hearing instruments when sounds leak from the vent or the seal between the earmold and the ear canal. In most cases, acoustic feedback is not audible. But when the in-situ gain of the hearing instrument is sufficiently high or when a larger than optimal size vent is used, the output of the hearing instrument generated within the ear canal can exceed the attenuation offered by the earmold/shell. The hearing instrument output then becomes unstable and the once-inaudible acoustic feedback becomes audible. Authors’ note: In this paper, we refer to the audible whistling tone as “feedback” even though readers should be aware that, technically, feedback occurs all the time in a hearing instrument.
Feedback limits the available gain for the wearer. For many wearers and the people around them, feedback is an annoyance and even an embarrassment. In addition, hearing instruments that are at the verge of feedback (i.e., sub-oscillatory feedback) may influence the frequency characteristics of the hearing instrument and lead to intermittent whistling.1 Indeed, as much as 24% of hearing instrument wearers reported dissatisfaction relative to whistling in the device.2 It is thus not unexpected that many researchers, engineers, and clinicians over the last several years have attempted to prevent and manage the occurrence of feedback. Readers are referred to Agnew3 for an excellent summary.
Despite the various approaches, including some using digital signal processing (DSP) techniques, all lead to some degrees of undesirable side-effects which may compromise comfort, sound quality, and/or speech intelligibility. The various aspects of feedback are reviewed in this article, including its generation, the principles of its management, the associated side-effects, and the ways in which these problems are designed to be resolved in a new digital hearing instrument.
Exploring Models of Feedback
A sound system is any entity that takes a sound input and produces an output. Using that definition, a hearing instrument is a physical system that takes sounds (i.e., input), amplifies them according to the hearing loss of the wearer (i.e., processing) so that the signals leave the hearing aid (i.e., output) at an appropriate loudness for the wearer.
Consequently, one can describe the behaviors of a hearing instrument using concepts that are commonly used in engineering control system theory.4 What follows is a simplified quantitative description of why and what happens when feedback occurs.
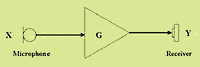
Fig. 1 shows a simple block diagram of a hearing instrument. The input signal (X) is amplified by a gain factor (G) that results in an output signal (Y). If the hearing aid/earmold provides a complete seal (i.e., no feedback path), the output signal (Y) would simply be determined by the gain of the hearing instrument and the input level (X). That is,
|
Equation 1: Y = GX |
|
|
|
Fig. 1. Block diagram of a hearing instrument. |
When a feedback path is present, a certain fraction (ß) of the output signal will leak back to the microphone. Fig. 2 shows a simple block diagram of a hearing instrument that allows some of the amplified sounds to leak back to its microphone (i.e., it has a feedback path). One can consider the feedback process as a looped sequence of events. First, the input signal X will create an output GX. During the first loop, a certain fraction (ß) of the output signal GX will leak back to the microphone and contribute to the input as ßGX. Thus, the combined input at the microphone will be (X + ßGX). Subsequently, the signal will be amplified by a factor G and contribute to the output signal. That is, the output of the hearing instrument after one loop becomes:
|
Equation 2: Y = GX + G (ßGX) |
|
|
| Fig. 2. Block diagram of a hearing instrument that allows some of the amplified sound to leak back to the microphone. |
As the output “loops” back to the microphone, output becomes progressively larger by a factor of Gß. After “n” number of loops, the output of the hearing instrument becomes:
Equation 3: Y = GX [1 + (Gß) + (Gß)2 +… + (Gß)n]
Equation 3 is an example of a power series and can thus be simplified into:
Equation 4: Y = GX/(1 – Gß)
Alternatively, an intuitive way of understanding Equation 4 is to consider that the output signal Y consists of two components. The first component is the amplified input signal, and the second component is the amplified feedback signal. The amplified input signal equals the input signal multiplied by the gain of the amplifier G (as per the basic hearing instrument diagram in Fig. 1). The feedback signal equals the fraction ß of the output signal Y (see Fig. 2). This feedback signal will be picked up by the microphone and be amplified by a factor G and contribute to the output signal as GßY. That is, the output of the hearing aid is:
Equation 5: Y = GX + GßY
By moving GßY to the left side of the equation and simplifying, we have:
Equation 6: Y (1- Gß)= GX
which, by dividing both sides by (1-Gß), we get the same result as shown in Equation 4 or: Y = GX / (1- Gß)
It turns out that Equation 4 is fundamental in understanding the factors that control feedback in a hearing aid. Note that, without the denominator (i.e., the part written beneath the divider line), Equation 4 is identical to Equation 1 for the hearing instrument without a feedback path (as per Fig. 1). Thus, it is this denominator that describes the feedback properties of a hearing aid. The elements in the denominator, G and ß, form the loop gain Gß (or open loop gain) which is the main determinant of possible feedback problems in a hearing instrument system.
Loop gain is obviously controlled by the gain (G) of the hearing instrument (i.e., that’s why you can sometimes eliminate feedback by reducing gain). On the other hand, the magnitude of ß is affected by many factors that may or may not be controllable. For example, while the amount of leakage from the vent can be controlled, intermittent leakage from jaw movement, presence of reflective surfaces close to the hearing instrument, room reverberation, and change of head position can also change the feedback path and affect the magnitude of ß. This means that the magnitude and frequency response of the feedback path may not be stationary.
One can see that if ß is zero (i.e., no leakage), the term Gß will be zero (0). The denominator will be 1 and the value of Y is solely determined by the values of G and X. In these cases where the denominator takes a positive value (>0), the hearing aid system is said to be stable and no audible feedback occurs (this is known as the Nyquist Stability Criterion). On the other hand, if the value of ß increases or if the gain of the amplifier increases (or both), the value of Gß increases. This, in turn, decreases the value of the denominator (1-Gß) and the output of the system increases. However, as the value of Gß approaches 1, the denominator approaches 0 and the system becomes unstable. In this case, audible feedback occurs and the output signal Y increases until it reaches the maximum output of the hearing instrument or when its gain is reduced through activation of the compression system.
Equation 4 also shows that, for the same leakage (ß), the occurrence of feedback is primarily determined by the gain (G) of the hearing instrument. As G increases, the risk of feedback increases as Gß approaches 1 (and the denominator approaches 0). Obviously, as G increases, the output GX also increases. However, one must realize that a high output does not always require high gain. A high input (X) with a low gain can also result in a high output.
Feedback Control Methods
Because audible feedback is a sign of instability of the hearing instrument system, Equation 4 suggests that there are two possible solutions to regain stability. One solution is to control the signal feeding back to the microphone by controlling the leakage factor ß. The other is to reduce gain (G) of the hearing instrument. The following describes ways in which feedback reduction has been implemented.
|
|
| Fig. 3. Effect on the input-gain curve during feedback management (Fb) on a linear hearing aid. Reducing gain to control feedback in linear hearing aids causes a reduction of gain across all frequencies and at all inputs. |
Preventive practice: Preventive measures to ensure that the wearer is given the best condition to utilize the available gain on the hearing instrument, includes:
- Ensuring an accurate ear impression;
- Ensuring proper orientation of the receiver in the ear canal;
- Avoiding cerumen in the ear canal or on the receiver opening;
- Ensuring that no cracks are found in the tubing, and
- Using an appropriate vent size, etc.
These practices are well known, and are targeted at controlling the potential feedback path ß. They should be exercised regardless of the availability of any anti-feedback or feedback cancellation algorithms on the hearing instrument.
Acoustic approaches: Most dispensing professionals are familiar with controlling feedback by reducing the leakage of sounds through the hearing instrument/earmold system. Attempts, such as restricting the vent diameter and/or increasing the diameter/girth of the first bend area of the earmold/hearing aid shell, are the first steps and represent the most frequently employed acoustic approaches.
However, these approaches may also affect the available gain from the hearing instrument. Kuk5 provided data on the maximum insertion gain of a single-channel linear power BTE hearing instrument as the diameter of a parallel Select-A-Vent (SAV) was adjusted from 0 to 3 mm. As much as 25 dB of gain change at 250 Hz and 10-15 dB above 1000 Hz was noted. Such findings could be modified if a multichannel hearing instrument were used instead.
Acoustic approaches are also aimed at managing the potential feedback path b. While these attempts can be effective, they may also lead to other side effects. For example, decreasing the vent diameter may lead to decreased ventilation of the occluded ear canal, alteration of the frequency response of the hearing aid, decreased flow of natural low frequencies through the vent, poorer subjective sound quality and increased perception of occlusion during vocalization.6 Furthermore, increasing the canal diameter of the earmold may lead to physical discomfort. In rare cases, soreness and abrasion of the ear canal may result.
Gain reduction in linear instruments: Most hearing instruments are manufactured with greater gain in the high frequencies. Unfortunately, the typical feedback path also provides less attenuation at high frequencies than at low frequencies. Therefore, the risk of audible feedback is highest in the higher frequency range.
One common method to control feedback is to lower the high frequency gain of the hearing instrument through the use of tone control or low pass filtering. However, gain in the higher frequency (and adjacent) regions is also compromised with this approach. Speech intelligibility may suffer as a consequence. Alternative approaches like the use of a notch filter (e.g., Agnew7), damping of the resonant frequency, phase shifting (e.g., Preves et al.8) and frequency shifting (e.g., Bennett et al.9), or reducing gain in one or more filters in a filter bank (e.g., Lunner et al.10) are more precise in controlling feedback with less effect on nearby frequencies. Obviously, the extent that this is true is dependent on the bandwidth of the filters.
There is an additional problem with managing feedback in linear hearing instruments. Because these devices provide the same gain at all input levels, gain reduction that is applied to a frequency region will be effective at all input levels. This means that soft sounds, as well as medium-level sounds, will be affected to the same extent. Speech intelligibility at all input levels may be affected (Fig. 3). Although the feedback frequency may originate from limited frequency regions, a wearer with a single-channel linear hearing instrument will have to lower the overall gain across all frequencies to minimize feedback.
Gain reduction in nonlinear instruments: A nonlinear (or compression) device provides less gain as input increases. Because feedback management in these instruments is also accomplished by reducing gain in the frequency region where feedback occurs, the same side-effects associated with feedback management in linear hearing instruments can occur.
There is one exception. Whereas, in a linear hearing instrument the gain at all input levels is affected, one may design a nonlinear hearing instrument so that only gain for the lowest input level may be affected. This is because the gain of a nonlinear aid is maximum at the lowest input level, and it decreases as input increases. By lowering this maximum gain via an increased compression threshold, feedback is controlled without affecting gain at higher input levels.11 This is an effective and practical method to control feedback and has been used in digital hearing instruments (e.g., Senso).12 Although the intelligibility of soft speech may be compromised, intelligibility for conversational speech is preserved. Fig. 4 shows the effect of feedback management on the input-gain curves of such a nonlinear hearing instrument. Note that only gain for the softer sounds are affected in the nonlinear aid.
An assumption behind the “gain reduction” approach to feedback management is that there is only one fixed feedback frequency. In reality, such an assumption is seldom true. Typically, there is more than one frequency at which instability occurs. Suppressing one frequency may create feedback at another frequency.3 Furthermore, as was indicated earlier, the feedback path is not stationary; it is dynamically modified by the state of the hearing instrument wearer. Consequently, feedback may still occur in real-life even though it is controlled in the clinic.
Feedback Strategies in DSP Instruments
Digital techniques provide additional possibilities for addressing the feedback problem. However, because of the vigorous computational requirements of such feedback reduction algorithms, many DSP hearing instruments utilize the methods described in the previous paragraphs. Despite such constraints, a number of DSP-based feedback cancellation algorithms have been attempted on hearing instruments to control feedback.
Principles of feedback cancellation: Fig. 2 shows that feedback occurs because amplification of the feedback signal (GßX) results in system instability. If the characteristics of this feedback signal are known, a filter can be generated that has a response characteristic similar to that of the feedback path. By subtracting the estimated feedback signal from the input, one may obtain a virtually feedback-free system. This is the principle behind modern feedback cancellation theory. Egolf & Larson13 described this principle in detail.
Although theoretically sound, the early feedback cancellation method described by Egolf & Larson13 was based on filters with one fixed response. As discussed previously, movement of the hearing instrument in the ear canal during jaw movements, changes in the reflective surfaces around the head (such as a telephone placed over the hearing aid14), etc., alter the feedback path characteristics. Consequently, feedback may still occur in real-life. A variable filter system that adapts to the changes in the characteristics of the feedback path is required.
Adaptive feedback cancellation: The first adaptive feedback cancellation systems designed for hearing instruments were developed around 1990.15,16 Instead of a fixed filter, a feedback cancellation system that constantly monitors the feedback path is used in order to update the characteristics of the adaptive cancellation filter. In earlier systems, the hearing instrument generated low-level noise as the input signal to the amplifier. Continuous correlation analyses were performed between the original noise signal entering the receiver and the microphone in order to provide a precise estimate of the feedback signal. The results of the correlation analyses were then used to continuously modify the transfer function of the adaptive filter towards the transfer function of the feedback path. Subtracting the estimated feedback signal from the microphone signal (which contains the real feedback signal) led to a cancellation of the feedback signal and thereby reduced the effective feedback factor (ß in Fig. 2).
The advantage of the adaptive algorithm is that no fixed filters are used and no compromises in usable gain are made. These algorithms reported an improvement of 5-10 dB of additional usable insertion gain before feedback.17 Furthermore, slow changes in the feedback path characteristics18 are also managed properly.
|
|
| Fig. 4. Effect on the input-gain curve during feedback management (Fb) on a nonlinear hearing aid. Note the difference in effect across input levels between the linear and nonlinear hearing aids. |
Despite its relative effectiveness, several problems prevented widespread acceptance of this system. One problem was the vigorous computational demand of the correlation analysis. To estimate the feedback path accurately, correlation analyses need to be performed continuously or at brief regular intervals. Considering the level of chip technology at that time, it was difficult to implement such a commercial system that was both cosmetically and functionally acceptable.
Another disadvantage with this approach is that the low-level noise used in the correlation was audible to most hearing instrument wearers. This was annoying to some wearers and, in practice, limited the use of these feedback canceling hearing instruments to people who had severe-to-profound losses. Recently, feedback cancellation systems that use sounds in the environment to estimate the feedback path have been described.19 These may solve the problem with audible measuring noise, since no artificial noise is present.
However, there may be remaining problems associated with artifacts and response speed of the cancellation method. It was mentioned earlier that correlation analyses are performed to estimate the feedback path. This is based on the assumption that a feedback signal is a highly correlated version of the original signal. If high correlation is observed, but the duration of the correlation analysis is short, the system may suggest the presence of feedback when in real-life no such feedback has occurred. This is an artifact of the analysis algorithm. In real-life, most speech and music signals are highly correlated on a short-term basis but not on a long-term basis. Thus, short-term correlation analysis on speech and music could result in cancellation of some signals, and could even lead to unpleasant sound quality and loss of intelligibility. This suggests that long-term correlation (i.e., slow-acting feedback path estimation) should be used to avoid such artifacts.
On the other hand, if the feedback cancellation algorithm takes a long time to cancel the feedback signal, it may not be able to handle the sudden changes in the characteristics of the feedback path. Audible feedback may still result until the feedback cancellation algorithm has successfully estimated and cancelled the feedback signal. For example, a telephone handset placed next to the ear will result in whistling that may last several seconds before the feedback cancellation algorithm is effective in abating the annoying signal. This is undesirable and the successful algorithm should (ideally) handle sudden changes in the feedback path.
To summarize, existing methods to reduce feedback include approaches to minimize leakage and reduce available gain. These methods may limit feedback, but can also lead to discomfort and loss of intelligibility/sound quality. Current DSP methods of adaptive feedback cancellation hold promise, but may also produce unwanted artifacts.
New DSP Feedback Solutions
Advances in miniaturization technology have allowed the use of a smaller, more powerful chip to implement an adaptive feedback algorithm in the Senso Diva for controlling feedback in real-life situations. The current algorithm includes several proprietary patent-pending elements, and Widex test results indicate over 10 dB more usable gain with little or no side-effects as those described previously. Because of the use of the chip design and its DSP implementation, the adaptive feedback algorithm in the instrument is active at all times while maintaining a low current drain. What follows is a description of the two principal components of the algorithm—the feedback path simulator and the dynamic cancellation optimizer.
Feedback path simulator (FPS): The feedback path simulator is designed to estimate the characteristics of the feedback signal in order to generate a cancellation signal. In contrast to previous attempts of using an external noise source, the FPS uses the incoming acoustic signal to drive the correlation process. Great effort was made to establish a time window of suitable length where correlation analyses are performed in order to avoid estimation errors of the feedback path (i.e., misinterpretation of speech/music as feedback). Hearing instrument wearers do not have to listen to the external noise that was described in the previous paragraphs.
Fig. 5 shows how the system works. The incoming microphone signal (A) is continuously correlated to the amplified signal entering the receiver (B) at a sampling rate of 32 kHz in order to estimate the signal feeding back from the receiver to the microphone. A cancellation signal (C) is generated which is sent to the summer (+) to cancel the feedback signal at the microphone. As the characteristics of the feedback path changes, the characteristics of the cancellation signal also changes. In order to obtain a stable analysis, an analysis window of approximately 5-10 seconds was chosen. The result of the analysis is updated for each new sample (i.e., 32,000 times per second).
|
|
| Fig. 5. Block diagram showing the two principal components of the Diva feedback cancellation algorithm: the feedback path simulator (FPS) and the dynamic cancellation optimizer (DCO). |
As previously mentioned, the advantage of this approach is that no fixed filter is used to affect the usable gain at any frequency or at any input levels. The bandwidths of the filter or the number of channels within the hearing instrument have no effect on the precision of the cancellation process because a cancellation signal is generated and added to the microphone signal prior to the band-split filters. Furthermore, since it is an inverse replicate of the feedback path, more than one feedback frequency can be canceled. Because the feedback path simulator is adaptive in nature, it automatically incorporates any changes of the characteristics of the feedback path that may occur over time.
A cautionary note is necessary. The FPS process is purposely designed to have an adaptation time of 5-10 s in order to avoid potential artifacts when speech and music are the incoming signals. When the characteristics of the feedback signal do not vary too much over time, the adaptive process has enough time to converge and create an exact “feedback cancellation signal’ with a high degree of precision. This would completely eliminate the feedback signal. However, if the characteristics of the feedback signal path vary considerably over time, the adaptive process may not have enough time to converge completely to yield an exact feedback cancellation signal. Indeed, this average estimate may deviate substantially from the characteristics of the momentary feedback signal to result in incomplete feedback cancellation.
|
|
| Fig. 6. Maximum gain before audible feedback without the feedback cancellation unit, and with both components of the feedback cancellation unit. Note that 10-12 dB more usable gain is available with the active feedback cancellation unit. |
Dynamic Cancellation Optimizer (DCO): The limitations of the FPS led to the development of the dynamic cancellation optimizer (DCO) algorithm. When the wearer is chewing or yawning, additional sound leakage occurs as the shape of the ear canal is altered. When a telephone is held close to the hearing instrument, the reflective surface close to the ear is changed. These situations represent some of the situations during which the feedback path and, consequently, the feedback signal is changed quickly. Because of the slow nature of the FPS, it may not be able to generate the “feedback cancellation signal” fast enough. As a consequence, feedback may occur in those instances until the FPS has estimated an accurate feedback signal and cancelled it. And, if the characteristics of the feedback signal do not stabilize (as in the wearer who constantly moves his/her jaw), feedback may never be canceled. Obviously, this can be annoying for the wearer.
An effective feedback cancellation algorithm should also be able to accommodate rapid changes in the feedback path. The DCO is a patent-pending, fast-acting mechanism that is designed to continuously estimate the attenuation characteristics of the feedback path in each of the frequency channels. From that, an estimate of the maximal gain in each frequency channel is calculated. Because it does not produce signals that are inserted into the signal path, its action can be very fast without producing the artifacts mentioned earlier. If the feedback path changes rapidly (e.g., a telephone brought to the ear), the DCO is designed to quickly and temporarily limit the low-input gain in the channels that produce the audible feedback. This allows the FPS time to recalculate the new feedback path and cancels the feedback signal without gain reduction. Because the DCO operates on specific channels, channel bandwidths could affect the specificity of its action; however, this should not be a concern in this instrument, as it uses 15 channels that are 1/3 octave wide.
Both FPS and DCO are active at all times. However, depending on the nature of the stimulus conditions and the requirements for the feedback mechanism, the action of one component may be more dominant over the other at any time. Fig. 6 shows that the combined effects of the FPS and DCO allow as much as 10-12 dB more usable gain before feedback occurs.
Conclusion
Acoustic feedback can be minimized through appropriate preventive and acoustic measures. Digital signal processing brings additional possibilities that far exceed the capability of traditional approaches.
|
Use of a Feedback Cancellation Algorithm During Fittings A feedback test is an integral component of the fitting procedure for the Diva DSP hearing instrument. Because experience with the feedback cancellation algorithm has been positive with minimal artifacts in a majority of situations, it is recommend that the algorithm remain active at all times. Depending on the individual characteristics and the test environment, an active feedback cancellation unit allows over 10 dB more usable gain than an inactive cancellation unit. On the other hand, deactivation of the feedback algorithm may prevent the occurrence of rare and unforeseen artifacts arising from certain types of music. An active feedback cancellation state is especially necessary for wearers who require a high amount of usable gain from the hearing instrument. In less critical situations, an active feedback cancellation algorithm could be advantageous for people who desire more venting/leakage from their hearing aid/earmold for improved subjective preference, including the occlusion effect. This could also be beneficial for those with soft ear canal skin and/or straight ear canal geometry and experience problems with their custom hearing instrument “working its way out” due to jaw movements. Additionally, this feature could be useful for pediatric fittings for those younger than age 10. Rapid growth of their ear canals20,21 and pinna/concha size as the child grows older leads to increased risk of feedback with the same earmold. The dispensing professional can perform the automatic feedback test from either the portable programmer (SP3) or the Compass software (v. 3.1). Testing should be done in a quiet environment to avoid extraneous sounds from confounding the test results. The signals are used to initialize the adaptive filter and to estimate the attenuation of the feedback path in each frequency channel. Output from the receiver that leaks back to the microphone through the acoustic feedback path is used to calculate the transfer properties of the feedback path. The feedback test provides two important pieces of information: it assesses the suitability of the shell/earmold fit and it initializes the system. Assessing the shell/earmold fit: Results of the feedback test indicate if the current earmold/shell provides a sufficient seal to retain the necessary gain for amplification of normal speech to the wearer’s comfortable listening level. This information may allow for a larger vent than is traditionally used, thereby reducing the occlusion effect and improving the subjective quality of the hearing instrument. However, a larger vent may reduce the effectiveness of the noise reduction and directional microphone systems. The advantage of the feedback test is that its results allow the dispensing professional to make an informed choice on the necessary vent diameter according to individual preferences and properties of the ear canal and auricle. Results of the feedback test also reflect the range of usable gain before audible feedback occurs. However, it is important to realize that the results apply only to the condition of the test situation during the feedback test. In a different situation (e.g., when a person’s mouth is open or when a telephone is placed over the ear), the hearing instrument’s acoustic path may become unstable and result in audible feedback. If one were to set the upper gain limit where feedback occurs to the value determined during the feedback test, the hearing instrument may be at the verge of acoustic oscillations all the time (sub-oscillatory feedback). This could alter the frequency response of the hearing aid.1 Furthermore, any movement of the jaw could send the hearing instrument into audible feedback. In order to avoid this, the practice of including a “feedback margin” was adopted in Senso Plus and Diva hearing instruments. The feedback margin represents the dB gain below the level where audible feedback occurs. For example, a feedback margin of 6 dB means that the maximum gain is set 6 dB below where audible feedback occurs. Initializing the system: The result of the feedback test also serves to initialize the feedback path simulator. That is, it sets the initial parametric settings of the digital filter so that it can generate the cancellation signal. The parameter values are stored in the memory of the hearing instrument and are activated every time the hearing instrument is switched on. The adaptive feedback cancellation process starts with that estimate as the first estimation of the feedback path. If there is no change in the condition in which the hearing instrument is worn in real-life, the FPS will take minimal time to cancel the feedback signal. If there is a change in the characteristics of the feedback path from the estimated one, the adaptive nature of the FPS will fine tune its parametric settings to cancel the feedback signal. The actual readjustment time depends on the closeness of the estimated feedback path and the actual feedback path. The greater the difference, the longer it takes the adaptive process to “zero in” on an accurate estimation. Thus, while the adaptive nature of the cancellation process would cancel any feedback signals, feedback tests conducted under more real-life conditions would be expected to yield better initial estimates of the feedback path and improve the effectiveness of the feedback cancellation process. For the same reason, it is important to redo the feedback test when the earmold or shell is modified so that a new set of initial values are stored. |
This article was submitted to HR by Francis Kuk, PhD, director of audiology at Widex Hearing Aid Co, Long Island City, NY, and Carl Ludvigsen, MS, director of audiology, and Thomas Kaulberg, PhD, research engineer at Widex ApS, Vaerloese, Denmark. Correspondence can be addressed to HR or Francis Kuk, Widex Hearing Aid Co, 35-53 24th St, Long Island City, NY 11106-4116; email: [email protected].
References
1. Cox RM. Combined effects of earmold vents and suboscillatory feedback on hearing aid frequency response. Ear Hear. 1982;3:12-17.
2. Kochkin S. Subjective measures of satisfaction and benefit: establishing norms. Seminars in Hearing. 1997; 18(1):37-48.
3. Agnew J. Acoustic feedback and other audible artifacts in hearing aids. Trends in Amplification. 1996;1(2):45-82.
4. Egolf D. Review of the acoustic feedback literature from a control system point of view. In G Studebaker & F Bess’ (eds) Vanderbilt Hearing Aid Report: State-of-the Art Research Needs. Upper Darby, Pa: Monographs in Contemporary Audiology, 1982: 94-103.
5. Kuk F. Maximum usable real-ear insertion gain with ten earmold designs. J Am Acad Audiol. 1994;5:44-51.
6. Kuk F. Perceptual consequences of venting in hearing aids. Brit J Audiol. 1991; 25:163-169.
7. Agnew J. Application of a notch filter to reduce acoustic feedback. Hear Jour. 1993; 46, 37-40.
8. Preves D, Sigelman J, LeMay P. A feedback stabilizing circuit for hearing aids. Hear Instrum. 1986; 37(4):34, 36-41, 51.
9. Bennett M, Srikandan S, Browne L. A controlled feedback hearing aid. Hear Aid Jour. 1980; 33(7):12, 42.
10. Lunner T, Hellgren J, Arlinger S, Elberling C. A digital filter bank hearing aid: Three digital signal processing algorithms—user preference and performance. Ear Hear. 1997;18:373-387.
11. Kuk F. Recent approaches to fitting nonlinear hearing aids. In RJ Roeser, M Valente & H Hosford-Dunn’s (eds) Audiology: Diagnosis, Treatment, and Practice Management. Vol. II. New York: Thieme Publisher. 2000:261-290.
12. Sandlin R. Introducing a completely digital hearing instrument. Hear Jour. 1996;49 (4):45-49.
13. Egolf D, Larson V. Acoustic feedback suppression in hearing aids. Rehab R & D Progress Reports. Washington, DC: Dept. of Veteran Affairs, 1984: 163-164.
14. Kates J. The problem of feedback in hearing aids. J Comm Disorders. 1991; 24:223-235.
15. Bustamante D, Worrall T, Williamson M. Measurement and adaptive suppression of acoustic feedback in hearing aids. Proc. ICASSP. 1989: 2017-2020.
16. Dyrlund O, Bisgaard N. Acoustical feedback margin improvements in hearing instruments using a prototype DFS (Digital Feedback Suppression) system. Scand Audiol. 1991; 20:49-53.
17. Henningsen L, Dyrlund O, Bisgaard N, Brink B. Digital Feedback Suppression (DFS). Scand Audiol. 1994; 23:117-122.
18. Engebretson A, French-St.George M, O’Connell M. Adaptive feedback stabilization of hearing aids. Scand Audiol. 1993; 22:56-64.
19. Hellgren J, Lunner T, Arlinger S. System identification of feedback in hearing aids. J Acoust Soc Amer. 1999; 105:3481-3496.
20. Kruger B. An update on the external ear resonance in infants and young children. Ear Hear. 1987; 8: 333-336.
21. Feigin J, Kopun J, Stelmachowicz P, Gorga M. Probe-tube microphone measures of ear canal sound pressure levels in infants and children. Ear Hear. 1989; 10: 254-258.